Qua các bài học trước, chúng ta đã nắm được các thao tác xử lý cơ bản với ảnh số và cách tương tác, thay đổi giá trị của từng điểm ảnh. Trong nhóm bài này, bạn đọc và tôi sẽ cùng nhau tìm hiểu thêm một số phương pháp biến đổi ảnh số cơ bản như: phép dịch, phép xoay, thay đổi kích thước, lật ảnh hay cắt ảnh số.

1.Phép dịch

Phương pháp đầu tiên mà chúng ta sẽ tìm hiểu là phép dịch ảnh. Phép dịch cho phép dịch chuyển bức ảnh, hay nói cách khác là dịch chuyển ma trận theo trục tung, và trục hoành. Bằng cách sử dụng phương pháp này, bức ảnh có thể dễ dàng di chuyển lên, xuống, qua trái, qua phải theo cách mà chúng ta mong muốn. Ta sẽ cùng nhau phân tích cách sử dụng dưới đây:

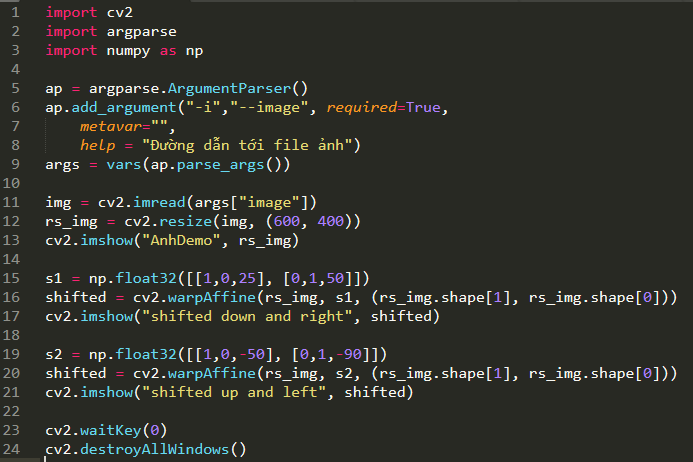
Dòng 1-13, khai báo thư viện sử dụng, và định nghĩa tham số truyền vào và đọc ảnh như ví dụ đã được trình bày trong các bài học trước.

Phép dịch ảnh được thực hiện dòng 15-17. Chúng ta bắt đầu bằng định nghĩa dịch chuyển là s1 – ma trận chứa thông tin về số điểm ảnh ta muốn dịch chuyển qua phải hoặc trái, lên trên hoặc xuống dưới. Thông tin này sau đó sẽ được áp dụng vào bức ảnh cần thực hiện biến đổi.

Ta có thể thấy rằng cấu trúc định nghĩa dịch chuyển là một ma trận gồm 2 thành phần:

[1, 0, tx]: tx là số lượng điểm ảnh ta muốn dịch bức ảnh qua trái hoặc phải. tx < 0 sẽ dịch bức ảnh qua trái và tx > 0 sẽ dịch bức ảnh phải

[0, 1, ty]: ty là số lượng điểm ảnh ta muốn dịch bức ảnh lên trên hoặc xuống dưới, ty < 0 dịch bức ảnh lên trên và ngược lại

Như vậy, chúng ta thấy rằng định nghĩa tx = 25 và ty = 50 sẽ dịch bức ảnh qua 25 điểm ảnh về phía bên phải và dịch bức ảnh xuống 50 điểm ảnh.

Sau khi định nghĩa ma trận dịch chuyển, phép dịch sẽ được chính thức thực hiện ở dòng 16 qua hàm cv2.warpAffine. Tham số đầu tiên hàm này nhận vào là bức ảnh ta muốn biến đổi, sau đó là ma trận dịch được định nghĩa – s1. Cuối cùng là tham số về chiều của bức ảnh đầu vào (số cột và số dòng). Bạn đọc có thể thử nghiệm thêm nhiều cách dịch khác nhau như ví dụ dòng 19-21. Kết quả chúng ta thu được như sau:

2.Phép xoay

Phương pháp thứ hai chúng ta tìm hiểu là phép xoay ảnh. Phương pháp này cho phép ta xoay ảnh theo một góc độ được định nghĩa

Dòng 1-13 định nghĩa và đọc ảnh như ở các ví dụ trước. Để có thể xoay một bức ảnh, chúng ta đặc biệt cần chú ý tìm ra tọa độ tâm mà ta muốn xoay bức ảnh, do đó opencv hỗ trợ người dùng định nghĩa dễ dàng tâm điểm này. Dòng 15-16, ta lấy kích thước bức ảnh và chia đôi để được tọa độ điểm chính giữa của bức ảnh. Thay vì phải định nghĩa ma trận xoay numpy như ở phép dịch, opencv cung cấp hàm cv2.getRotationMatrix2D – nhận 3 tham số đầu vào gồm tọa độ tâm điểm ta muốn xoay hình, sau đó là giá trị góc ta muốn xoay từ tâm và cuối cùng là kích thước bức ảnh.

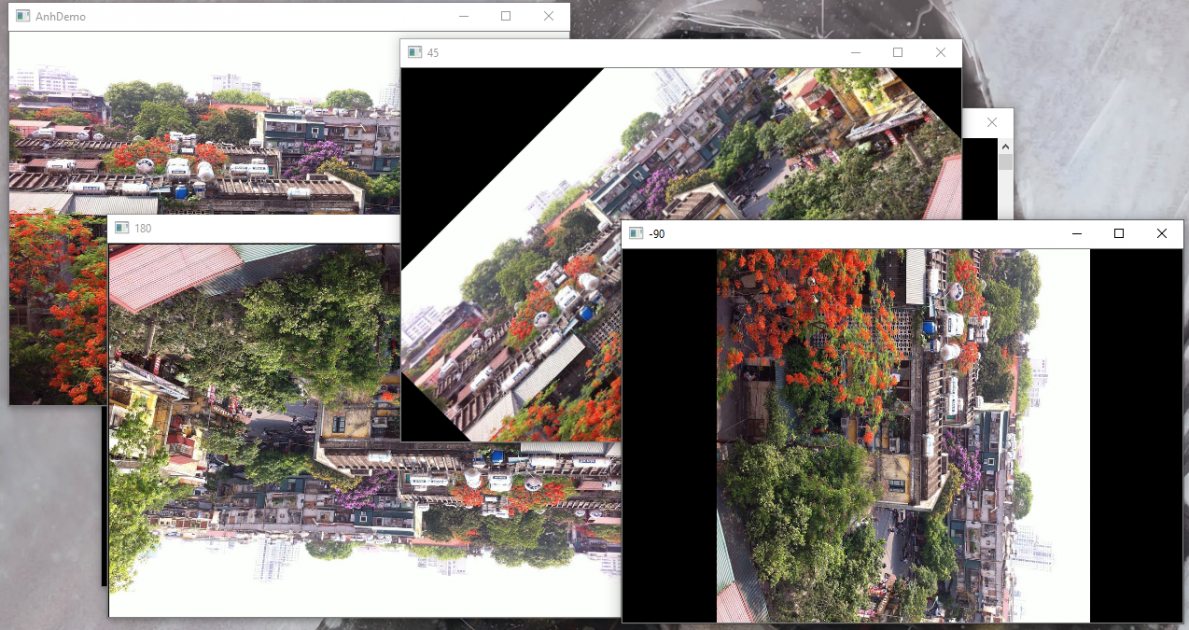
Như vậy, với tham số thứ hai là 45, ta hiểu rằng bức ảnh ban đầu được xoay theo góc 45 độ và hình ảnh xoay giữ nguyên kích thước ban đầu khi tham số thứ ba là 1.0 và bị chia đôi khi bằng 0.5 hay gấp đôi với giá trị là 2.0. Tuy nhiên việc thay đổi kích thước ảnh sẽ được bàn luận ở phần sau của bài học.

Khi mà ta đã có được ma trận định nghĩa phép xoay, ta thực hiện biến đổi ảnh qua hàm cv2.warpAffine ở dòng 19. Kết quả mà chúng ta thu được như sau:

3.Thay đổi kích thước

Sau phép dịch và phép xoay ảnh, chúng ta sẽ tiếp tục tìm hiểu phương pháp thay đổi kích thước ảnh. Chắc hẳn bạn đọc không hề xa lạ với hàm cv2.resize, tuy nhiên chúng ta sẽ nghiên cứu kĩ hơn về các tham số sử dụng trong hàm qua ví dụ sau:

Dòng 1-13 thực hiện thao tác quen thuộc: khai báo thư viện, định nghĩa tham số, đọc và hiển thị bức ảnh. Phần thú vị bắt đầu ở dòng 15-16, để có thể thay đổi kích thước ảnh số, chúng ta cần chú ý tới tỉ lệ khung hình – mối quan hệ giữa số hàng và số cột của ma trận biểu diễn hình ảnh. Nếu bạn đọc không chú ý tới hai yếu tố này, sai sót trong tỉ lệ khung hình thay đổi kích thước sẽ dẫn đến kết quả ảnh hiển thị không theo ý muốn.

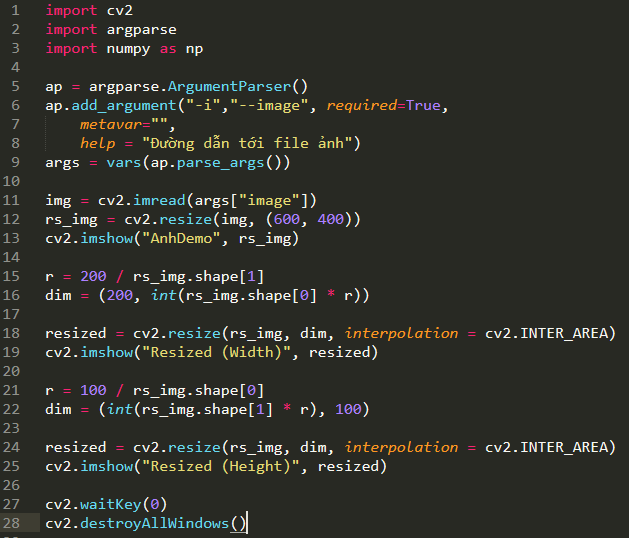
Việc tính toán tỉ lệ khung hình được xử lý tại dòng 15. Ở đây, chúng ta định nghĩa ảnh mới có số cột là 200 điểm ảnh. Để có thể tính tỉ lệ khung hình – số hàng ma trận mới so với hiện tại, ta định nghĩa giá trị r = 200 chia số cột – rs_img.shape[1]. Khi đã có tỉ lệ khung hình, chúng ta tính chiều của bức ảnh sau khi thay đổi kích thước qua dòng 16. Như vậy, ta thu được số cột ở ảnh mới là 200, ta tìm số hàng của ma trận mới bằng cách nhân giá trị hàng ma trận cũ với tỉ lệ r

Bức ảnh được thay đổi kích thước thực hiện ở dòng 18, qua hàm cv2.resize. Tham số đầu tiên là bức ảnh gốc bạn muốn thay đổi kích thước, tham số thứ hai là kích thước ảnh mới và cuối cùng là phương thức interpolation – thuật toán thực hiện thay đổi kích thước ảnh. Bạn đọc có thể thay thế cv2.INTER_AREA bằng một số tùy chọn khác như cv2.INTER_LINEAR, cv2.INTER_CUBIC hay cv2.INTER_NEAREST. Bên cạnh đó, bạn cũng có thể thay đổi kích thước bức ảnh theo tỉ lệ giữa số hàng và số cột ma trận hoặc ngược lại. Kết quả chúng ta thu được sau khi thay đổi kích thước bức ảnh với hai trường hợp: số cột = 200 và số hàng 100

4.Lật ảnh

Nếu bạn đọc thắc mắc làm thế nào để tạo hình ảnh như đổ bóng, hay hình ảnh phản chiếu thì phép lật ảnh sẽ hỗ trợ bạn thực hiện các tác vụ này. Phép dịch ở trên cho phép ta di chuyển toàn bộ bức ảnh theo hệ tọa độ, thì phương pháp lật ảnh mà opencv hỗ trợ giúp ta lật ảnh qua lại quanh trục tọa độ. Chúng ta bắt đầu ngay với ví dụ sau:

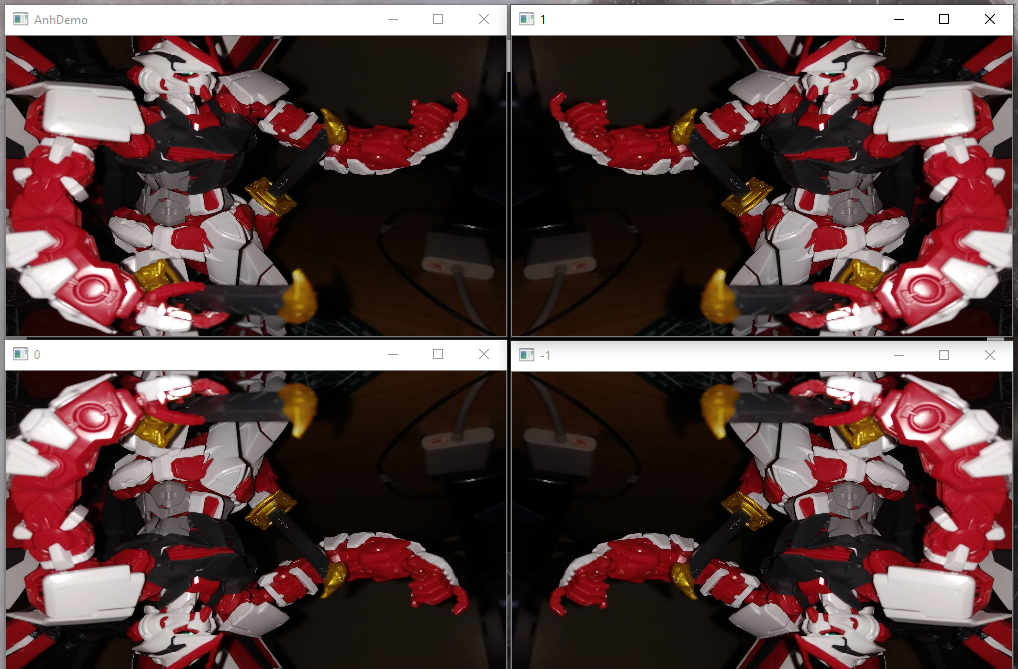
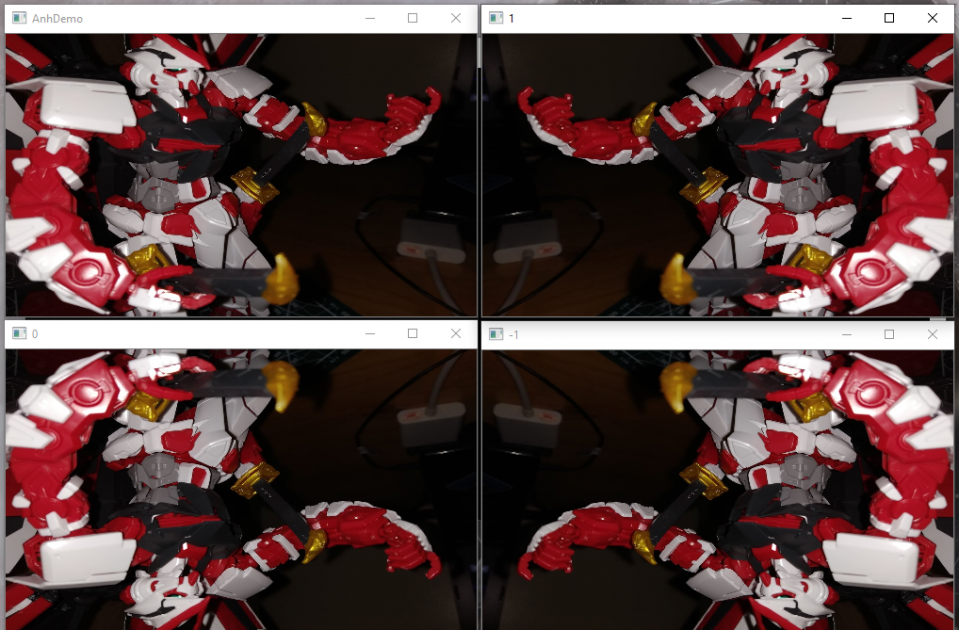
Chúng ta sẽ bắt đầu ngay vào với hàm cv2.flip dòng 15, phương thức này nhận vào hai tham số: đầu tiên là bức ảnh ta muốn lật, và thứ hai là flip code sử dụng để quyết định ta sẽ lật bức ảnh theo cách nào.

Ý nghĩa giá trị flip code:

0: lật bức ảnh theo trục tung

1: lật bức ảnh theo trục hoành

-1: lật bức ảnh theo cả hai trục

Đây có lẽ là phương pháp biến đổi cơ bản nhất mà chúng ta tìm hiểu. Sau khi thực thi, chúng ta thu được kết quả sau:

5.Cắt ảnh

Để có thể loại bỏ các thành phần thừa trong một bức ảnh, ta sử dụng phương pháp cắt ảnh. Phương pháp này rất quen thuộc với bạn đọc và đã được đề cập trong bài học trước. Chúng ta thực hiện cắt ảnh thông qua sự hỗ trợ từ thư viện numpy bằng việc khai báo tọa độ vùng mà ta muốn giữ lại

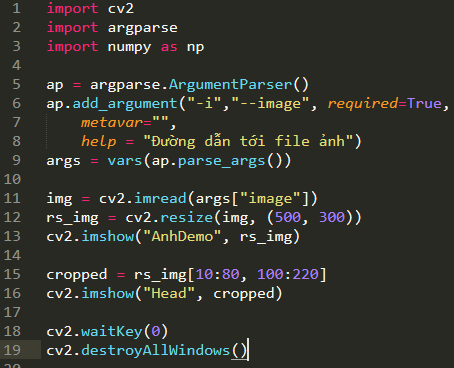
Quá trình cắt ảnh được thực hiện ở dòng 15, chúng ta thực hiện việc định nghĩa tọa hình chữ nhật cắt ảnh từ tọa độ bắt đầu từ (100,10) tới (220,80). Ta cần cung cấp 4 giá trị để có thể thực hiện phương pháp cắt ảnh:

y – bắt đầu: trục tung, y = 10

y – kết thúc: trục tung, y = 80

x – bắt đầu: trục hoành, x = 100

x – kết thúc: trục hoành, x = 220

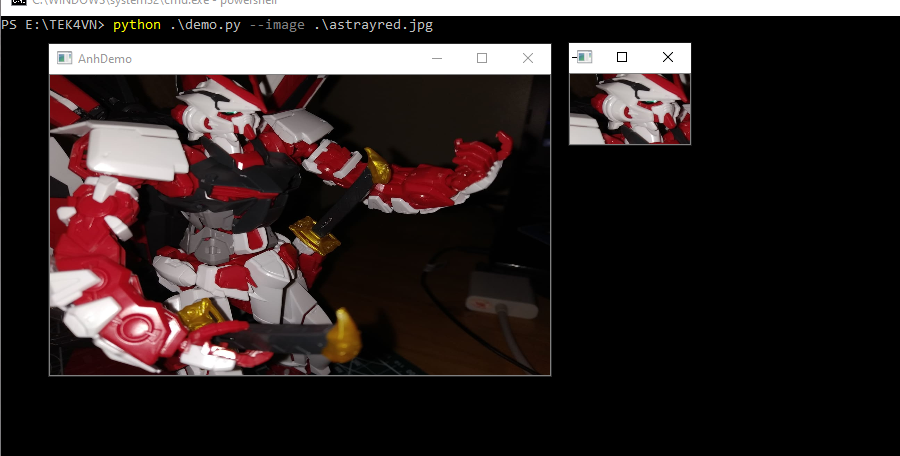
Như vậy, ta có thể cắt được vùng ảnh chứa đầu của gundam astray red:

Ở bài tiếp theo, chúng ta sẽ cùng nhau tìm hiểu một số phép toán trên ảnh.